Af hverju deilum við ekki með núll?

Lesendur gætu velt því fyrir sér hvers vegna ég helgi heila grein í svona banal mál? Ástæðan er ótrúlegur fjöldi nemenda (!) sem stundar aðgerðina frjálslega undir nafninu. Og ekki bara nemendur. Stundum grípa ég og kennarar. Hvað munu nemendur slíkra kennara geta í stærðfræði? Ástæðan fyrir því að skrifa þennan texta var strax samtal við kennara sem deiling með núll var ekki vandamál fyrir ...

Með núlli, já, fyrir utan vesenið með alls ekki neitt, því við þurfum í raun ekki að nota það í daglegu lífi. Við förum ekki að versla núll egg. „Það er ein manneskja í herberginu“ hljómar einhvern veginn eðlilegt og „núll fólk“ hljómar gervi. Málfræðingar segja að núll sé utan málkerfisins.

Við getum líka verið án núllsins á bankareikningum: notaðu bara - eins og á hitamæli - rautt og blátt fyrir jákvæð og neikvæð gildi (athugaðu að fyrir hitastig er eðlilegt að nota rautt fyrir jákvæðar tölur og fyrir bankareikninga það er á hinn veginn, vegna þess að skuldfærslan ætti að kalla fram viðvörun, svo rautt er mjög mælt með).

Með því að setja núll inn sem náttúrulega tölu snertum við vandamálið við aðgreining Höfuðtölur od heimilishald. Innan 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, …..

kraftur tölunnar er sá sami og talan á staðnum þar sem hún stendur. Annars er það nú þegar í röðinni 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, ….

Fjöldi eintónasetta kemur í öðru sæti, fjöldi setta með tveimur þáttum í þriðja sæti, og svo framvegis. Við verðum að útskýra hvers vegna, til dæmis, númerum við ekki sæti íþróttamanna í keppnum frá grunni. Þá fengi sá sem komst í fyrsta sæti silfurverðlaun (gull fékk núllsætið) og svo framvegis. Nokkuð svipað aðferð var notuð í fótbolta — ég veit ekki hvort lesendur gera sér grein fyrir því að „league one“ þýðir "fylgja þeim bestu." ", og núll deildin er kölluð til að verða "meiri deildin".

Stundum heyrum við þau rök að við þurfum að byrja frá grunni, því það er þægilegt fyrir upplýsingatæknifólk. Í framhaldi af þessum hugleiðingum ætti að breyta skilgreiningunni á kílómetra - það ætti að vera 1024 m, vegna þess að þetta er fjöldi bæta í kílóbæti (ég ætla að vísa í brandara sem tölvunarfræðingar þekkja: „Hver ​​er munurinn á nýnema og nemandi í tölvunarfræði og fimmta árs nemandi þessarar deildar? að kílóbæti er 1000 kílóbæti, það síðasta - að kílómetri er 1024 metrar")!

Annað sjónarmið, sem nú þegar ætti að taka alvarlega, er þetta: við mælum alltaf frá grunni! Það er nóg að skoða hvaða kvarða sem er á reglustikunni, á heimilisvog, jafnvel á klukkuna. Þar sem við mælum frá núlli og hægt er að skilja talningu sem mælingu með víddarlausri einingu, þá ættum við að telja frá núlli.

Þetta er einfalt mál, en...

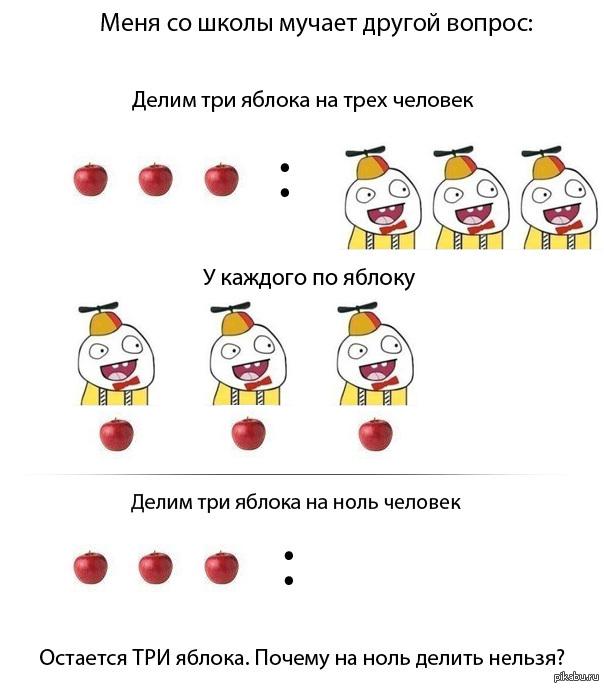
Sleppum almennum rökum og snúum aftur að deilingu með núlli. Málið er einfalt og það væri einfalt ef ekki væri fyrir ... hvað svo? Hugsum og reynum. Hversu mikið getur það verið - einn deilt með núlli? Við skulum sjá: 1/0 = x. Margfaldaðu báðar hliðar með nefnara vinstri hliðar.

Við fáum 1=0. Eitthvað er að! Hvað gerðist? Ah giska! Sú forsenda að það sé hlutfall af einingu og núll leiðir til mótsagnar. Og ef ekki er hægt að deila einum með núll, þá getur önnur tala. Ef þú, lesandi, yppir öxlum og veltir því fyrir þér hvers vegna höfundurinn (það er að segja ég) skrifar um slíkar þversögn, þá ... er ég mjög feginn!

Formúluna 0/0 = 0 væri hægt að verja á þrjóskum grundvelli, en hún stangast á við þá reglu að niðurstaðan af því að deila tölu með sjálfri sér sé jöfn einum. Algjörlega, en töluvert ólík eru slík tákn eins og 0/0, °/° og þess háttar í reikningi. Þeir þýða ekki neina tölu, heldur eru táknrænar merkingar fyrir tilteknar raðir af ákveðnum gerðum.

Í rafverkfræðibók fann ég áhugaverðan samanburð: að deila með núll er alveg jafn hættulegt og háspennurafmagn. Þetta er eðlilegt: Lögmál Ohms segir að hlutfall spennu og viðnáms sé jafnt og straumi: V = U / R. Ef viðnám væri núll myndi fræðilega óendanlegur straumur flæða í gegnum leiðarann ​​og brenna alla mögulega leiðara.

Ég skrifaði einu sinni ljóð um hættuna við að deila með núll fyrir alla daga vikunnar. Ég man að dramatískasti dagurinn var fimmtudagurinn, en það er leitt fyrir alla mína vinnu á þessu sviði.

Þegar þú deilir einhverju með núll

Mjög snemma á mánudaginn

Vika hvað gerðist bara

Þér hefur þegar mistekist hrapallega.

Þegar þriðjudagseftirmiðdegi

Þú setur núll í nefnarann

Ég skal segja þér þá, þú hefur rangt fyrir þér

Slæmur stærðfræðingur!

Þegar í gegnum núllið, í gegnum rangfærslu,

Langar að skilja á miðvikudaginn

Þú munt lenda í miklum vandræðum

Þú ert með hey og vatn í hausnum!

Bartek nokkur var með okkur.

Hann var á skjön við reglurnar.

Á fimmtudag er það deilanlegt með núlli.

Hann er ekki lengur á milli okkar!

Ef undarleg löngun nær tökum á þér

Deilið með núll á föstudaginn

Ég skal vera heiðarlegur, ég skal vera heiðarlegur:

Slæm byrjun á þessari helgi.

Þegar það er núll, einhvers staðar á laugardaginn

Skilrúmið verður þitt (ekki feitletrað)

Krjúpa undir kirkjugirðingunni.

Þetta er upprisa þín.

Viltu núll undir strikinu,

Gerðu frí á sunnudaginn

Komdu með krít, svart borð.

Skrifaðu: það er ekki deilanlegt með núlli!

Núll er tengt við tómleika og ekkert. Reyndar kom hann að stærðfræði sem stærð sem, þegar hún er bætt við einhverja, breytir henni ekki: x + 0 = x. En nú birtist núll í nokkrum öðrum gildum, einkum sem skala byrjun. Ef fyrir utan gluggann er hvorki jákvætt hitastig né frost, þá ... er þetta núll, sem þýðir ekki að það sé ekkert hitastig. Núllklassa minnisvarði er ekki sá sem hefur verið rifinn í langan tíma og er einfaldlega ekki til. Þvert á móti er það eitthvað eins og Wawel, Eiffelturninn og Frelsisstyttan.

Ja, mikilvægi núllsins í stöðukerfi er varla hægt að ofmeta. Veistu, lesandi, hversu mörg núll Bill Gates er með á bankareikningnum sínum? Ég veit það ekki, en mig langar í helminginn. Svo virðist sem Napóleon Bonaparte hafi tekið eftir því að fólk er eins og núll: það öðlast merkingu með stöðu. Í As the Years, As the Days Pass eftir Andrzej Wajda springur hinn ástríðufulli listamaður Jerzy: "Philister er núll, nihil, ekkert, ekkert, nihil, núll." En núll getur verið gott: "núll frávik frá norminu" þýðir að allt gengur vel og haltu því áfram!

Snúum okkur aftur að stærðfræðinni. Núll er hægt að leggja saman, draga frá og margfalda refsilaust. „Ég þyngdist um núll kíló,“ segir Manya við Anya. „Og þetta er áhugavert, því ég léttist jafn mikið,“ svarar Anya. Svo við skulum borða sex núll skammta af ís sex sinnum, það mun ekki skaða okkur.

Við getum ekki deilt með núll, en við getum deilt með núll. Auðvelt er að afhenda disk af núllbollum til þeirra sem bíða eftir mat. Hversu mikið mun hver fá?

Núll er ekki jákvætt eða neikvætt. Þetta og númerið ekki jákvættи ekki neikvætt. Það uppfyllir ójöfnuðina x≥0 og x≤0. Mótsögnin "eitthvað jákvætt" er ekki "eitthvað neikvætt", heldur "eitthvað neikvætt eða jafnt og núll". Stærðfræðingar munu, þvert á reglur tungumálsins, alltaf segja að eitthvað sé "jafnt núlli" en ekki "núll". Til að réttlæta þessa framkvæmd höfum við: ef við lesum formúluna x = 0 "x er jafnt núlli" þá lesum við x = 1 "x er jafnt og einum", sem gæti verið kyngt, en hvað með "x = 1534267" ? Þú getur heldur ekki tengt stafnum 0 tölugildi⁰né hækka núll í neikvætt veldi. Aftur á móti geturðu rótað núll að vild... og útkoman verður alltaf núll. 

Veldisfall y = a^x, jákvæður grunnur a, verður aldrei núll. Af því leiðir að það er enginn núlllogaritmi. Reyndar er logaritmi a til grunns b veldisvísirinn sem grunnurinn þarf að hækka upp í til að fá logaritma a. Fyrir a = 0 er enginn slíkur vísir og núll getur ekki verið grunnur lógaritmans. Hins vegar er núllið í "nefnara" Newtons tákns eitthvað annað. Við gerum ráð fyrir að þessar samþykktir leiði ekki til mótsagna.

rangar sannanir

Deiling með núll er algengt viðfangsefni fyrir rangar sannanir og það gerist jafnvel hjá reyndum stærðfræðingum. Leyfðu mér að gefa þér tvö af uppáhaldsdæmunum mínum. Hið fyrra er algebruískt. Ég mun "sanna" að allar tölur eru jafnar. Segjum að það séu tvær tölur sem eru ekki jafnar. Því er annar þeirra stærri en hinn, látum a > b. Gefum okkur að c sé mismunur þeirra

c \uXNUMXd a - b. Þannig að við höfum a - b = c, þaðan sem a = b + c.

Við margföldum báða hluta þess síðarnefnda með a - b:

a² – ab = ab + ac – b2 – bc.

Ég þýði ak á vinstri hlið, auðvitað man ég eftir því að hafa skipt um merki:

a² - ab - ac = ab - b2 - bc.

Ég útiloka algenga þætti:

A (a-b-c) \uXNUMXd b (a-b-c),

Ég deili og hef það sem ég vildi:

a = b.

Og reyndar enn skrítnara, vegna þess að ég gerði ráð fyrir að a > ​​b, og ég fékk að a = b. Ef í dæminu hér að ofan er auðvelt að þekkja „svindl“, þá er það ekki svo auðvelt í rúmfræðilegu sönnuninni fyrir neðan. Ég mun sanna að ... trapisan er ekki til. Myndin sem almennt er kölluð trapisa er ekki til.

En segjum fyrst að það sé til eitthvað sem heitir trapisa (ABCD á myndinni hér að neðan). Það hefur tvær samsíða hliðar ("basar"). Við skulum teygja þessar undirstöður, eins og sést á myndinni, þannig að við fáum samsíða. Skár þess skipta hinni ská trapisunnar í hluta þar sem lengdir eru táknaðar x, y, z, eins og í mynd 1. Út frá líkingu samsvarandi þríhyrninga fáum við hlutföllin:

þar sem við skilgreinum:

Oraz

þar sem við skilgreinum:

Dragðu frá hliðar jafnréttis merktar með stjörnum:

 Ef við styttum báðar hliðar um x − z, fáum við – a/b = 1, sem þýðir að a + b = 0. En tölurnar a, b eru lengdir grunnanna í trapisunni. Ef summan þeirra er núll, þá eru þau líka núll. Þetta þýðir að mynd eins og trapisa getur ekki verið til! Og þar sem rétthyrningar, tíglar og ferningar eru líka trapisur, þá eru engir tíglar, ferhyrningar og ferningar, kæri lesandi, heldur ...

Giska Giska

Að deila upplýsingum er áhugaverðasta og mest krefjandi af fjórum grunnaðgerðum. Hér lendum við í fyrsta skipti á fyrirbæri sem er svo algengt á fullorðinsárum: "giskaðu á svarið og athugaðu síðan hvort þú hafir giskað rétt." Þetta er mjög viðeigandi orðað af Daniel K. Dennett ("Hvernig á að gera mistök?", í How It Is – A Scientific Guide to the Universe, CiS, Varsjá, 1997):

Þessi aðferð við að „giska“ truflar ekki fullorðinslíf okkar - kannski vegna þess að við lærum það snemma og að giska er ekki erfitt. Hugmyndafræðilega kemur sama fyrirbæri fram, til dæmis í stærðfræðilegri (algjörri) innleiðingu. Á sama stað „gátum“ við formúluna og athugum síðan hvort giska okkar sé rétt. Nemendur spyrja alltaf: „Hvernig þekktum við mynstrið? Hvernig er hægt að taka það út?" Þegar nemendur spyrja mig þessarar spurningar breyti ég spurningu þeirra í brandara: "Ég veit þetta vegna þess að ég er fagmaður, því mér er borgað fyrir að vita." Nemendum í skólanum er hægt að svara í sama stíl, bara alvarlegri.

Hreyfing. Athugið að við byrjum samlagningu og skriflega margföldun með lægstu einingunni og deilingu með hæstu einingunni.

Sambland af tveimur hugmyndum

Stærðfræðikennarar hafa alltaf bent á að það sem við köllum aðskilnað fullorðinna sé sameining tveggja hugmyndafræðilega ólíkra hugmynda: Húsnæði i aðskilnaður.

Sá fyrsti (Húsnæði) á sér stað í verkefnum þar sem erkitýpan er:

Deila-deila Þetta eru verkefni eins og:

? (Við höldum upprunalegum stíl þessa vandamáls, tekin úr handbók Julian Zgozalewicz sem gefin var út í Krakow árið 1892 - złoty er Rhenish złoty, gjaldmiðillinn sem var í umferð í austurrísk-ungverska keisaradæminu fram í byrjun XNUMX. aldar).

Íhugaðu nú tvö vandamál með elsta stærðfræðikennslubók í pólsku, faðir Tomasz Clos (1538). Er það deild eða coupe? Leysa það eins og skólabörn á XNUMXth öld ættu að:

(Þýðing á pólsku yfir á pólsku: Það er kvart og fjórir pottar í tunnu. Pottur er fjórir lítrar. Einhver keypti 20 tunnur af víni fyrir 50 zł til viðskipta. Tollur og skattar (vörugjald?) verða 8 zł. Hversu mikið á að selja kvart til að vinna sér inn 8 zł?)

Íþróttir, eðlisfræði, samsvörun

Stundum í íþróttum þarf að deila einhverju með núll (markmiðahlutfall). Jæja, dómararnir taka á því einhvern veginn. Hins vegar, í abstrakt algebru, eru þeir á dagskrá. magn sem ekki er núllþar sem veldi er núll. Það er jafnvel hægt að útskýra það einfaldlega.

Lítum á fall F sem tengir punkt (y, 0) við punkt í planinu (x, y). Hvað er F², semsagt tvöföld framkvæmd á F? Núllfall - hver punktur hefur mynd (0,0).

Að lokum eru stærðir sem eru ekki núll, þar sem veldi er 0, næstum daglegt brauð fyrir eðlisfræðinga, og tölur á forminu a + bε, þar sem ε ≠ 0, en ε² = 0, kalla stærðfræðingar tvöfaldar tölur. Þeir koma fyrir í stærðfræðilegri greiningu og í mismunarúmfræði.

Enda er eitthvað í reikningi sem hefur deilingu með núll í að minnsta kosti nafninu. Það kemur frá samkvæmni. Látum Z tákna mengi heiltalna. Að deila menginu Z með p þýðir að við jöfnum hverri tölu (heiltölu) við nokkrar aðrar, nefnilega þeim sem munur þeirra er deilanleg með. Svo, þegar við höfum fimm tegundir af tölum sem samsvara tölunum 0, 1, 2, 3, 4 - mögulegar afgangar þegar deilt er með 5. Formúlan er skrifuð svona:

mod þegar munurinn er margfaldur.

Fyrir = 2 höfum við aðeins tvær tölur: 0 og 1. Að skipta heiltölum í tvo slíka flokka jafngildir því að skipta þeim í slétt og odda. Við skulum skipta um það núna. Mismunurinn er alltaf deilanlegur með 1 (hver heil tala er deilanleg með 1). Er hægt að taka =0? Við skulum reyna: hvenær er munur tveggja talna margfeldi af núll? Aðeins þegar þessar tvær tölur eru jafnar. Þannig að það er skynsamlegt að deila mengi heiltalna með núll, en það er ekki áhugavert: ekkert gerist. Þó skal áréttað að hér er ekki um talnaskiptingu að ræða í þeim skilningi sem þekkist úr grunnskóla.

Slíkar aðgerðir eru einfaldlega bannaðar, sem og löng og víð stærðfræði.

Hrísgrjón. 2. Auðkenning númera með samanburði

(hamur 5 og hamur 2)